road-of-leetcode
1029. 两地调度
解法 1 (greedy.js)
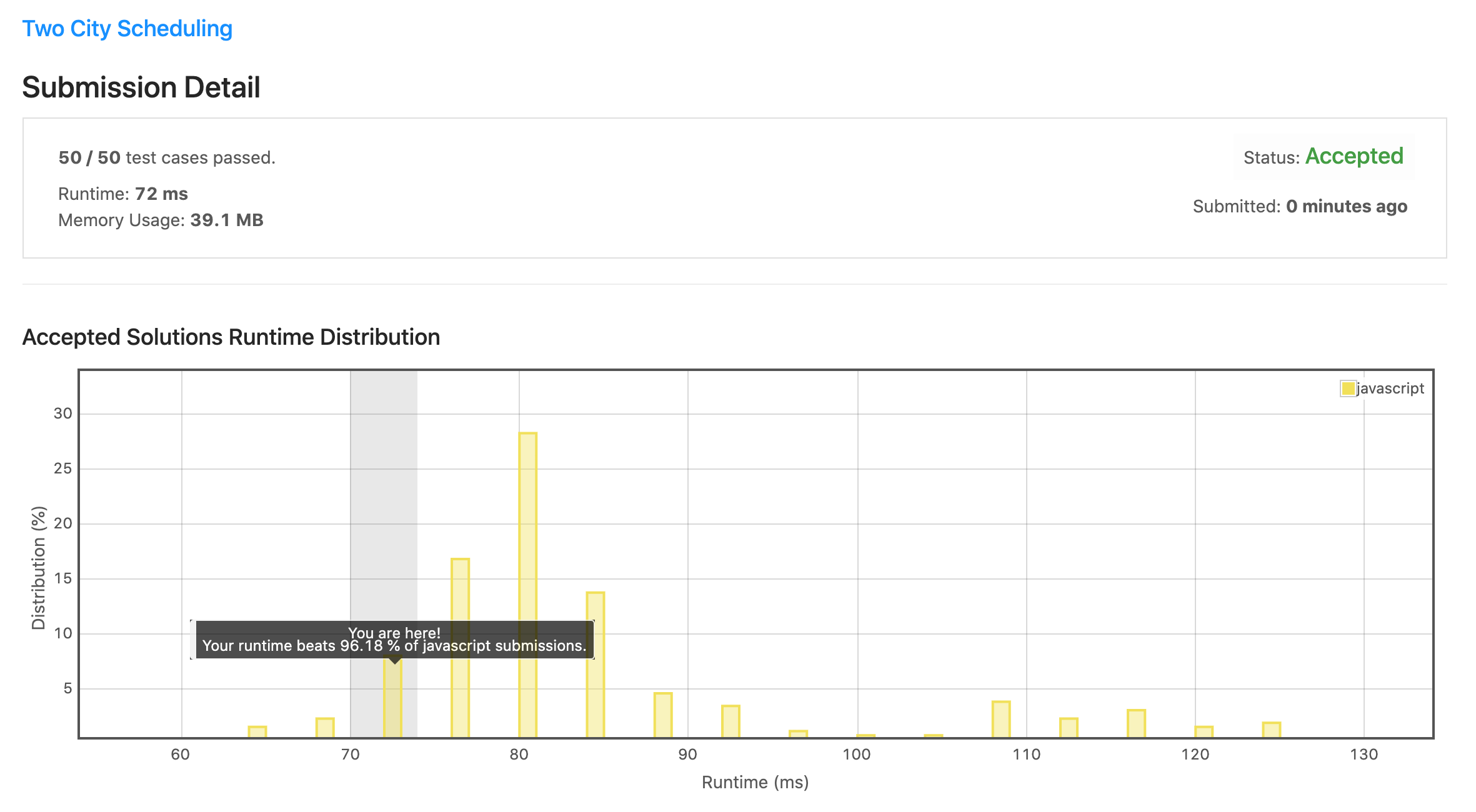
计算所有人去两地之间花费的差值, 排列后直接从中间分开, 各去自己更值得去的城市.
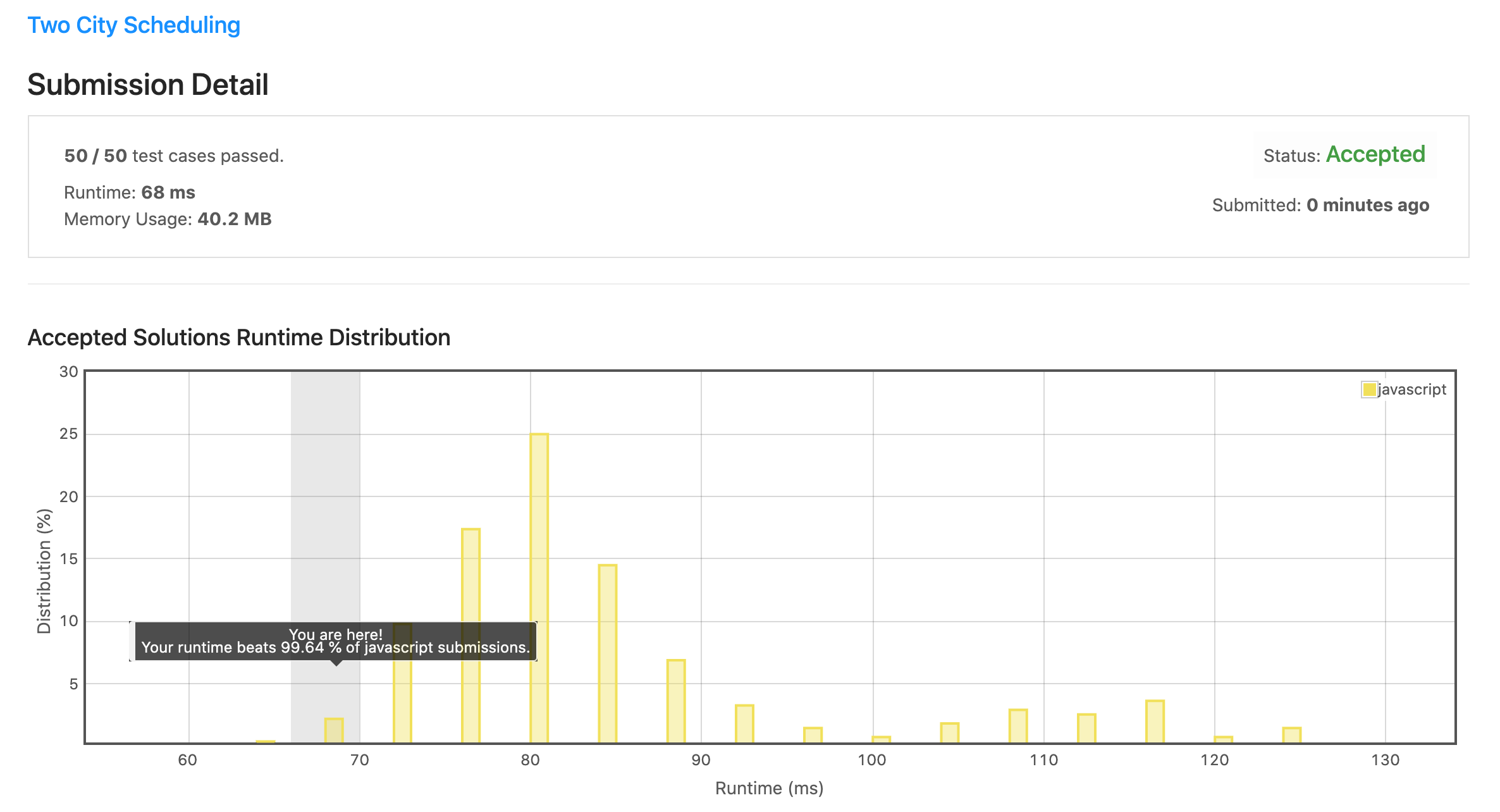
解法 2 (dynamic-programming.js)
根据题意, 可总结倒推规律:
最终结果 = min(
最后一个人去 A 的花费 + minCost(count(B) - count(A) === 1),
最后一个人去 B 的花费 + minCost(count(A) - count(B) === 1)
)
如果不追求效率, 实际上可以用上面的方法直接递归计算了.
为了方便书写, 我们将两地命名为甲、乙, 总共有 10 个人, 分别命名为 A B C D E F G H I J.
使用表格来递归计算各种情况, 其中横轴代表去乙的人数, 纵轴代表去甲的人数, 这样右下角的单元格即为去两地人数相等时的花费之和最小值了.
以相邻的四个单元格为例:
| n-2 的最优结果 | 前 n-1 个人中多一个去乙的最优结果 |
|---|---|
| 前 n-1 个人中多一个去甲的最优结果 | 当前的最优结果 |
进一步推理, 可得下图, 其中 0 的一行 / 列代表了 n 个人全去同一地, 没有人去另一地的情况, 因为总共只有 10 人, 所以最多只有 5 人去同一个地方, 故是一个 6x6 的表格:
| / | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 0 | / | A | AB | ABC | ABCD | ABCDE |
| 1 | A | AB | ABC | ABCD | ABCDE | ABCDEF |
| 2 | AB | ABC | ABCD | ABCDE | ABCDEF | ABCDEFG |
| 3 | ABC | ABCD | ABCDE | ABCEDF | ABCDEFG | ABCDEFGH |
| 4 | ABCD | ABCDE | ABCDEF | ABCDEFG | ABCDEFGH | ABCDEFGHI |
| 5 | ABCDE | ABCEDF | ABCDEFG | ABCDEFGH | ABCDEFGHI | ABCDEFGHIJ |